positional encoding

https://blog.csdn.net/m0_37605642/article/details/132866365

https://zhuanlan.zhihu.com/p/121126531

https://0809zheng.github.io/2022/07/01/posencode.html

https://machinelearningmastery.com/a-gentle-introduction-to-positional-encoding-in-transformer-models-part-1/

https://medium.com/@shravankoninti/transformers-attention-is-all-you-need-positional-encoding-485dcc1019fe

介绍

在所有语言中，词语的位置和顺序对于句子意思都是至关重要的，改变位置很可能就会改变语句的含义
对于传统的RNN模型，对于输入的序列都是顺序保存的，但是Transformer模型中，句子里面的词语都是同时进入网络进行处理，没有明确的关于单词在语句中的位置信息，为了记录原始的位置信息，Transformer引入了一个Positional Encoding来为每个单词添加一个额外的编码来表示它在序列中的位置

positional-insensitive

如上所说，RNN是对于位置敏感的，transformers是对位置不敏感的
是否对于位置敏感，我们可以通过更清晰的数学语言来进行解释和辅助理解
设模型为函数 ：

其中对于输入为一个词序列

输出结果为向量y。 对于x的任意置换，

都有

则模型f是关于位置不敏感的。

理想的位置编码应该具有以下的几个特点

1. 可以表示一个token在序列中的绝对位置
2. 序列长度不同的情况下，不同序列中的token的相对位置需要保持一致
3. 可以用来表示模型训练过程中从来没有看到过的句子长度

Transformer中位置编码的定义:

这里

其中

表示token的位置向量

为token的维度，论文中为512，t表示第几个token，i表示该token位置向量的第几个维度

根据sinusoid相关函数可以知道一个token的位置向量的越高的维度的波长越长，token之间的在越高维度的差别不大，
下面以可视化的形式展示这个效果，下图是序列长度50，位置编码维度128的位置编码的可视化结果：

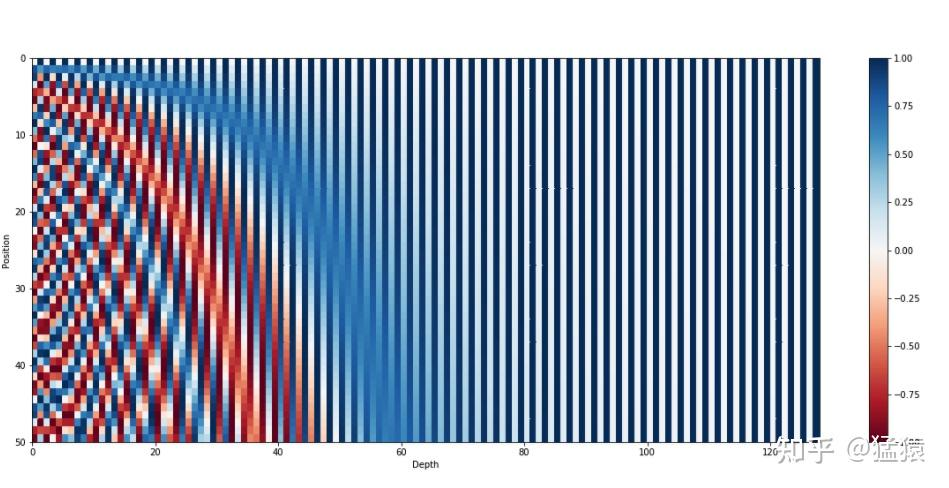
可以发现，由于sin/cos函数的性质，位置向量的每一个值都位于[-1, 1]之间。同时，纵向来看，图的右半边几乎都是蓝色的，这是因为越往后的位置，频率越小，波长越长，所以不同的t对最终的结果影响不大。而越往左边走，颜色交替的频率越频繁。

这里函数中使用较大的系数来拉大波长，主要为了防止存在后面的token会和之前的token位置编码出现重合
使用sin和cos来交替表示位置编码的相邻的维度主要是为了实现两个token的位置编码可以通过线性变换得到，这样位置编码的相对位置就有意义了

这里T表示线性变换矩阵，正是由于我们使用sin和cos交叉表示位置编码各个维度，通过向量的线性旋转变换公式可以得到